

All online polls use, by nature, convenience sampling. It's a poll on, titledĮvangelicals Want". Purchasing habits, or even the voting on American Show, those people in the shopping malls trying to survey you about your Unfortunately, they're rarely representative. Convenience samples are just what they sound like - convenient. Probably the most common is the so-called convenience Other methods do exist for finding samples of populations. Number of entire boxes of bulbs and test each bulb within those boxes.
To use cluster sampling, a quality control inspector might select a certain And all the bulbs are essentially the same, so thereĪren't any characteristics with which to stratify them. You don't have a complete list, so simple random samplingĭoesn't apply, and the bulbs are already in boxes, so you can't order them Suppose your company makes light bulbs, and you'd like to test the effectiveness One situation where cluster sampling would apply might be in manufacturing. We would number the clusters 1-6 and use technology to randomly select two Since we want a random sample of size four, we just select two of the clusters. With our visual, let's suppose the 12 individuals are paired up just as they That way, we just select a certain number of clusters. Up into groups ( clusters), and each cluster represents the population. In essence, we use cluster sampling when our population is already broken Sampling, we split the population up into groups (strata) based on some characteristic.Ī cluster sample is obtained by selectingĪll individuals within a randomly selected collection or group of individuals. Cluster SamplingĬluster sampling is often confused with stratified sampling, because theyīoth involve "groups". Typically passing by that spot and what sample size was needed. It would depend on the number of students

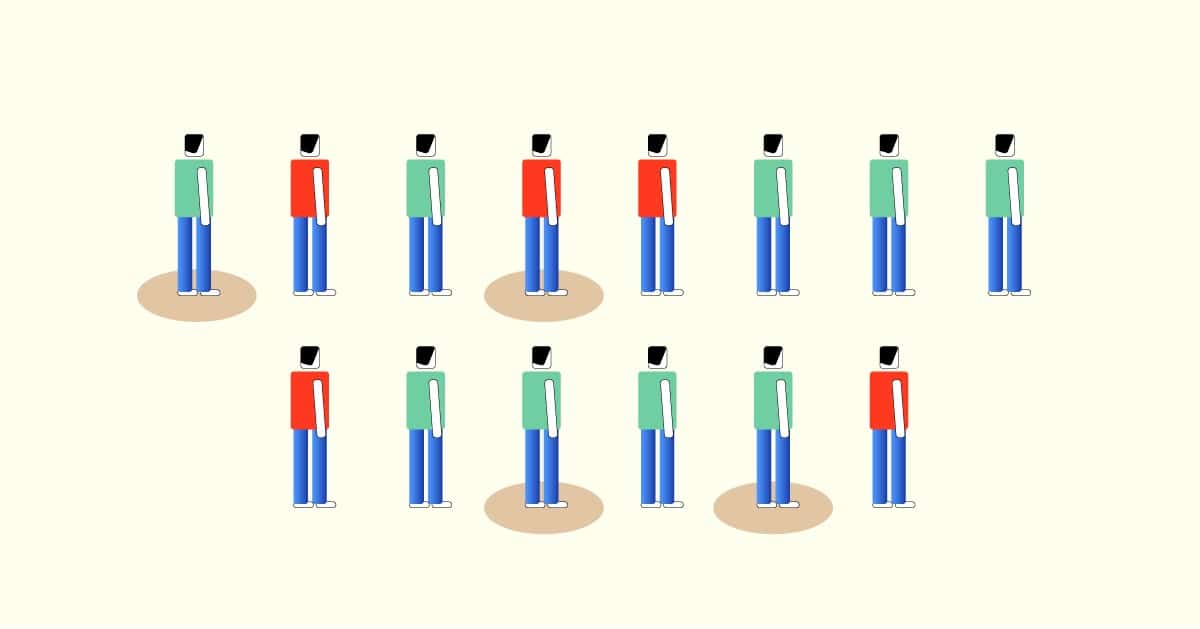
* Of course, choosing 10 here is just an example. We don't have access to the complete list, just stand at a corner and pick every 10th* person Students have often used this method when asked to survey a random sample of ECC students. Systematic sampling works well when the individuals are already lined up in order. In general we find k by taking N/ n and rounding The individuals sampled would then be 2, 5, 8, and 11. In our example, we want to use 3 for k? Can you see why? Think what would happen if weįor our starting point, we pick a random number between 1 and k. So to use systematic sampling, we need to first order our individuals, then select every kth. The first individual selected corresponds to a random number between Then we just need to make sure we get the same proportion out of 200, so multiply all of those by 200 (round to the nearest individual)ĥ0 and older: 0.054*200 = 11 Systematic SamplingĪ systematic sample is obtained by selecting every kth To do that, we need to first find the proportion in each group. We need to select a proportional number from each group. Since these groups are not the same size, we would not just sample 200/5 = 40 from each group. The Right-to-Know page on the ECC website has the following counts by age (as of ): We would want to get a representative sample from each age group. Suppose we want to sample 200 ECC students on a particular issue, where the responses might vary by age. Sample of 4 should have 1 blue, 1 green, and 2 reds.įor another take, watch this YouTube video: Working things out, we can see that a stratified (by color) random Individuals in the population are blue, so 1/4 of the sample should be blueĪs well. The number selected should be proportional. (Man, that's a weird word!) The key here is that Once we have the strata determined, we need to decide how many individuals We can easily separate the individuals by color. Visually, it might look something like the image below. Within each group should be similar in some way. Obtaining a proportional simple random sample from each group. The population into non-overlapping groups called strata and then Using some characteristic, and then take a proportional random sample fromĪ stratified sample is obtained by separating With this technique, we separate the population Do you remember how simple random sampling works? Visually, it's just numberingĮach individual and randomly selecting a certain number of them.


 0 kommentar(er)
0 kommentar(er)
